The Log-Approximate-Rank Conjecture Is False
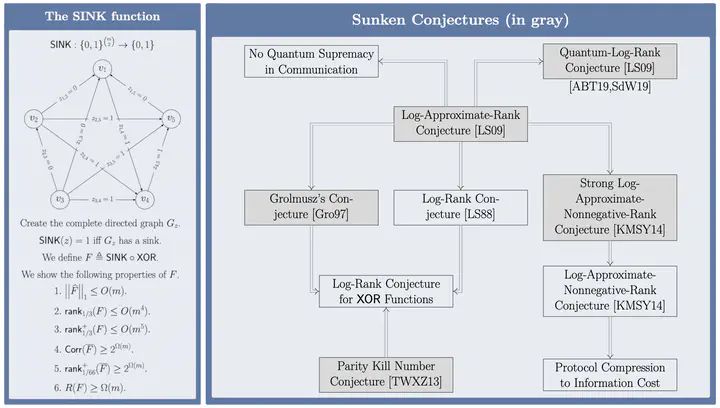 The SINK function, some of its properties and the conjectures it refutes.
The SINK function, some of its properties and the conjectures it refutes.
Abstract
We construct a simple and total Boolean function $F = f \circ \mathsf{XOR}$ on $2n$ variables that has only $O(\sqrt{n})$ spectral norm, $O(n^2)$ approximate rank and $O(n^{2.5})$ approximate nonnegative rank. (The approximate nonnegative rank has been improved to $O(n^2)$ in this paper by Mande and de Wolf.) We show it has polynomially large randomized bounded-error communication complexity of $\Omega(\sqrt{n})$. This yields the first exponential gap between the logarithm of the approximate rank and randomized communication complexity for total functions. Thus $F$ witnesses a refutation of the Log-Approximate-Rank Conjecture (LARC) which was posed by Lee and Shraibman [LS09] as a very natural analogue for randomized communication of the still unresolved Log-Rank Conjecture for deterministic communication. The best known previous gap for any total function between the two measures is a recent 4th-power separation by Göös, Jayram, Pitassi and Watson [GJPW17].
Additionally, our function $F$ refutes Grolmusz’s Conjecture [Gro97] and a variant of the Log-Approximate-Nonnegative-Rank Conjecture, suggested recently by Kol, Moran, Shpilka and Yehudayoff [KMSY14], both of which are implied by the LARC. The complement of $F$ has exponentially large approximate nonnegative rank. This answers a question of Lee [Lee12] and Kol et al. [KMSY14], showing that approximate nonnegative rank can be exponentially larger than approximate rank. The inner function $f$ also falsifies a conjecture about parity measures of Boolean functions made by Tsang, Wong, Xie and Zhang [TWXZ13]. The latter conjecture implied the Log-Rank Conjecture for $\mathsf{XOR}$ functions.
We are pleased to note that shortly after we published our results two independent groups of researchers, Anshu, Boddu and Touchette [ABT19], and Sinha and de Wolf [SW19], used our function $F$ to prove that the Quantum-Log-Rank Conjecture is also false by showing that $F$ has $\Omega(n^{1/6})$ quantum communication complexity.